|
|
Solving Equations Algebraically and Graphically
Objective:
In this lesson you learned how to solve linear
equations,
quadratic equations, polynomial equations, equations
involving radicals, equations involving fractions, and
equations involving absolute values.
Important Vocabulary Define each term or concept.
Equation A statement that two algebraic expressions are equal.
Extraneous A solution that does not satisfy the original equation.
x-intercept The point (a, 0) is an x-intercept of the graph if it is a
solution point of the
equation.
y-intercept The point (0, b) is a y-intercept of the graph if it is a
solution point of the
equation.
Point of intersection An ordered pair that is a solution of two
different equations. |
I. Equations and Solutions of Equations (Pages
38-39)
To solve an equation in x means to . . . find all the values of x
for which the solution is true.
The values of x for which the equation is true are called its
solutions .
An identity equation is . . . an equation that is true for every
real number in the domain of the variable.
A conditional equation is . . . an equation that is true for just
some (or even none) of the real numbers in the domain of the
variable.
A linear equation in one variable x is an equation that can be
written in the standard form ax + b = 0 , where a and b
are real numbers with a ≠ 0 .Example 1:
Solve 5(x + 3) = 35.
The solution is 4.
To solve an equation involving fractional expressions, . . .
find the least common denominator of all terms in the equation
and multiply every term by this LCD.
When is it possible to introduce an extraneous
solution?
When multiplying or dividing an equation by a variable
expression.
Example 2: Solve: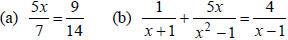

|
What you should learn
How to solve linear
equations |
| |
II. Intercepts and Solutions (Pages 39-41)
To find the x-intercepts of the graph of an equation, . . .
let y = 0 and solve the equation for x.
To find the y-intercepts of the graph of an equation, . . .
let x = 0 and solve the equation for y.
Example 3: For the equation 3x - 4y =12 , find:
(a) the x-intercept(s), and (b) the y-intercept(s).
(a) (4, 0)
(b) (0, - 3) |
What you should learn
How to find x- and
y-intercepts of graphs of
equations |
III. Finding Solutions Graphically (Pages 41-42)
To use a graphing utility to graphically approximate the
solutions of an equation , . . . (1) write the equation in general
form, y = 0, with the nonzero terms on one side of the equation
and zero on the other side; (2) use a graphing utility to graph the
equation. Be sure the viewing window shows all the relevant
features of the graph; (3) use the zero or root feature or the
zoom and trace features of the graphing utility to approximate
each of the x-intercepts of the graph.
Example 4: Use a graphing utility to approximate the solutions
of 3x2 -14x = -8 .
The solutions are 2/3 and 4.
|
What you should learn
How to find solutions of
equations graphically |
IV. Points of Intersection of Two Graphs (Pages
43-44)
To find the points of intersection of the graphs of two equations
algebraically, . . . solve each equation for y (or x) and set
the two results equal to each other. The resulting equation will be
an equation in one variable, which can be solved using standard
procedures.To find the points of
intersection of the graphs of two equations
with a graphing utility, . . . use the graphing utility to graph
both equations in the same viewing window and use the intersect
feature or the zoom and trace features to find the point or points
at which the two graphs intersect.
Example 5: Use (a) an algebraic approach and (b) a graphical
approach to finding the points of intersection of
the graphs of y = 2x2 - 5x + 6 and x - y = -6 .
(0, 6) and (3, 9) |
What you should learn
How to find the points of
intersection of two
graphs |
| |
V. Solving Polynomial Equations Algebraically
(Pages 45-46)
List four methods for solving quadratic equations:
1) Factoring
2) Using the Square Root Principle or Extracting Square Roots
3) Completing the Square
4) Quadratic Formula
To solve a quadratic equation by factoring, . . . write the
equation in general form with all terms collected on the left side
and zero on the right. Then factor the left side of the quadratic
equation as the product of two linear factors. Finally, find the
solutions of the quadratic equation by setting each factor equal to
zero.
Example 6: Solve x2 -12x = -27 by factoring.
The solutions are 3 and 9.
Using the Quadratic Formula to solve the quadratic equation
written in general form as ax2 + bx + c = 0 gives the solutions:
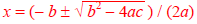
Example 7: For the quadratic equation 3x -16 =
-2x2 , find
the values of a, b, and c to be substituted into the
Quadratic Formula. Then find the solutions of the
equation. Round to two decimal places.
a = 2, b = 3, and c = - 16, OR a = - 2, b = - 3, and
c = 16
The solutions are - 3.68 and 2.18.
Example 8: Describe a strategy for solving the
polynomial
equation x3 + 2x2 - x = 2 . Then find the solutions.
First write the polynomial equation in general form with zero on the
right-hand side
of the equation. Then factor the polynomial by grouping to solve. The
solutions are
- 2, - 1, and 1. |
What you should learn
How to solve polynomial
equations |
| |
VI. Other Types of Equations (Pages 47-49)
An equation involving a radical expression can often be cleared
of radicals by . . . raising both sides of the equation to an
appropriate power.
When using this procedure, remember to check for
extraneous solutions , which do not satisfy the original
equation.
Example 9: Describe a strategy for solving the following
equation involving a radical expression:
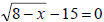 Add 15 to
both sides to isolate the radical expression. Then square both sides to
eliminate the radical. Finally, solve for x and check the solution in
the original
equation.
To solve an equation involving fractions, . . . multiply both
sides of the equation by the least common denominator of each
term in the equation to clear the equation of fractions.
Example 10: Solve: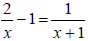
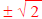
To solve an equation involving an absolute value,
. . .
remember that the expression inside the absolute value symbols
can be positive or negative, resulting in two separate equations to
be solved.
Example 11: Write the two equations that must be solved to solve
the absolute value equation 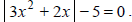
3x2 + 2x = 5 and - (3x2 + 2x) = 5 |
What you should learn
How to solve equations
involving radicals,
fractions, or absolute
values |
| |
Homework Assignment
Page(s)
Exercises |
|
|