|
|
Graph the rational function
|
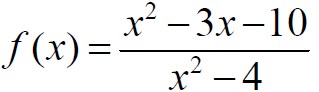
|
|
Steps |
Step 1: Find the domain of the rational function
Step 2: Write f(x) in lowest terms
Step 3: Locate the intercepts of the graph. The x-intercepts, if
any, of 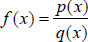 in lowest terms
satisfy the equation p(x)=0. The y-intercept, if there is one, is f(0) in lowest terms
satisfy the equation p(x)=0. The y-intercept, if there is one, is f(0)
Step 4: Test for symmetry. Replace x by −x in f(x). If f(−x)=f(x)there
is symmetry with respect to the y-axis; if f(-x)=-f(x) there is symmetry
with respect to the origin.
Step 5: Locate the vertical asymptotes. The vertical asymptotes,
if any, of 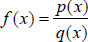 in lowest terms
are found by identifying the real zeros of q(x). Each zero of the
denominator gives rise to a vertical asymptote. in lowest terms
are found by identifying the real zeros of q(x). Each zero of the
denominator gives rise to a vertical asymptote.
Step 6: Locate the horizontal or oblique asymptotes, if any,
using the procedure given in page 2 of the hand-out. Determine the
points, if any, at which the graph of f(x)(in lowest terms) intersects
these asymptotes.
Step 7: Graph f(x) using graphing utility
Step 8: Use the results obtained in steps 1 through 7 to graph
f(x) by hand |
Exercise:
1. Domain :_________________________________________
2. 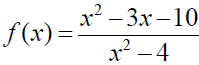 in lowest terms ____________________ in lowest terms ____________________
3. x intercept(s): _______________
4. y intercept(s): _______________
5.
a. Symmetry with respect to y axis (yes/no)?
b. Symmetry with respect to origin (yes/no)?
6. Vertical asymptote(s): ______________________________
7. Horizontal asymptote(s): ____________________________
8. Does the graph intersect the horizontal asymptote? If it does, at what
points?
9. Graph f(x) in the graphing utility
10. Use all the results above and draw f(x) by hand
|