|
|
Graph Linear Inequalities in Two Variables
VOCABULARY
Linear inequality in two variables The result of replacing the 5 sign in a
linear equation with <,≤,> or ≥
Solution of an inequality in two variables An ordered pair (x, y) that
produces a true statement when the values are substituted into an inequality in
two variables x and y
Graph of an inequality in two variables The set of points that represent all
solutions of the inequality
Half-plane Either half of the coordinate plane that is divided by the
boundary line of a linear inequality
Example 1 Check solutions of a linear inequality
Tell whether the ordered pair is a solution of 3x - 4y >
9.
a. (2, 0) b. (2, 21)
Solution
a.
3x - 4y > 9 Write inequality. 3( 2 ) - 4( 0 )
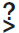 9 Substitute 2 for x and 0 for
y. 6 > 9 x Simplify. (2, 0) is not a solution of 3x - 4y > 9.
b.
3x - 4y > 9 Write inequality. 3( 2 ) - 4( -1 )
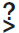9 Substitute 2 for x and -1
for y. 10 > 9 ✓ Simplify. (2, -1) is a solution of 3x - 4y > 9.
GRAPHING A LINEAR INEQUALITY IN TWO VARIABLES
Step 1 Graph the boundary line. Use a dashed line
for < or >, and use a solid line for ≤or ≥.
Step 2 Test a point not on the boundary line by
checking whether the ordered pair is a solution of the inequality.
Step 3 Shade the half-plane containing the point if
the ordered pair is a solution of the inequality. Shade the
other half-plane if the ordered pair is not a solution.
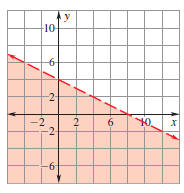
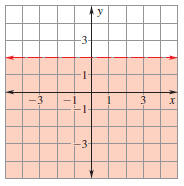
Example 2 Graph a linear inequality in two variables
Graph the inequality  .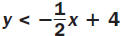
Solution
Step 1 Graph the equation 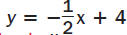 . The
inequality is <, so use a dashed line.
Step 2 Test (0, 0) in  .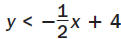
0 <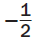 (0)+4
0 < 4 ✓
Step 3 Shade the half-plane that contains (0, 0)
because (0, 0) is a solution of the inequality.
Example 3 Graph a linear inequality in one variable
Graph the inequality x ≥ 4.
Solution
Step 1 Graph the equation x 5 4. The inequality is ≥, so use a
solid line.
Step 2 Test (0, 3) in x ≥ 4. You only substitute the x-coordinate
because the inequality does not have the variable y . 0 ≥ 4 x
Step 3 Shade the half-plane that does not contain (0, 3), because (0, 3)
is not a solution of the inequality.
Guided Practice Graph the inequality.
1. 2y + 4x > 8
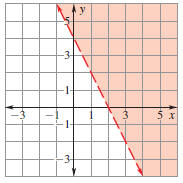
2. y < 2
|
