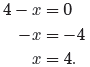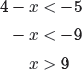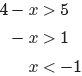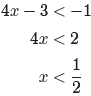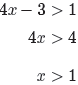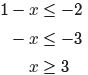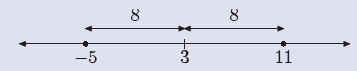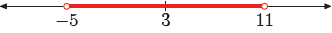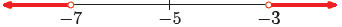|
|
Absolute Value Inequalities
 Example 13.
State the solution of each of the following inequalities. Example 13.
State the solution of each of the following inequalities.
a. |x| > −5
b. |x| > 0
c. |x| > 4
Solution:
a. The solution of |x| > −5 is all real numbers.
b. The solution of |x| > 0 is all real numbers except zero.
c. The solution of |x| > 4 is the set of all real numbers less than −4 or
greater than 4.
 Example 14.
Solve the inequality |4 − x| > −5 for x. Example 14.
Solve the inequality |4 − x| > −5 for x.
The left-hand side of the inequality |4 − x| > −5 is nonnegative, so the graph
of
y = |4 − x| must lie above or on the x-axis. The graph of the right-hand side of
|4−x| > −5 is a horizontal line located 5 units below the x-axis. Therefore, the
graph
of y = |4 − x| always lies above the graph of y = −5. Thus, all real numbers are
solutions of the inequality |4 − x| > −5.
We can verify our thinking with the graphing calculator. Load the left- and
right-hand
sides of the inequality |4 − x| > −5 into
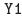 and and 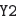 , respectively, as shown in , respectively, as shown in
Figure 6(a). From the ZOOM menu, select 6:ZStandard to produce the image
shown
in Figure 6(b).
As predicted, the graph of y = |4 − x| lies above the graph of y = −5 for all
real
numbers.
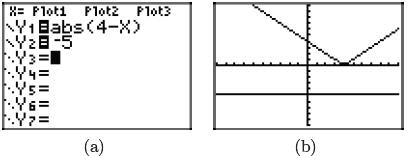
Figure 6. Using the graphing
calculator to solve |4 − x| > −5.
Intuitively, the absolute value of any number is always nonnegative, so |4−x| >
−5 for
all real values of x.
 Example 15.
Solve the inequality |4 − x| > 0 for x. Example 15.
Solve the inequality |4 − x| > 0 for x.
As we saw in Figure 6(b), the graph of y = |4 − x| lies on or above the
x-axis for
all real numbers. It “touches” the x-axis at the “vertex” of the “V,” where
|4 − x| = 0.
This can occur only if
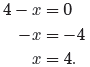
Thus, the graph of y = |4 − x| is strictly above the
x-axis for all real numbers except
x = 4. That is, the solution of |4 − x| > 0 is {x : x ≠ 4}.
 Example 16.
Solve the inequality |4 − x| > 5 for x. Example 16.
Solve the inequality |4 − x| > 5 for x.
In this example, the graph of the right-hand side of |4 − x| > 5 is a horizontal
line located 5 units above the x-axis. The graph of y = |4 − x| has the “V”
shape
shown in Figure 6(c). You can use the intersect utility on the graphing
calculator to
approximate the points of intersection of the graphs of y = |4 − x| and y = 5,
as we
have done in Figure 7(c) and (d). The calculator indicates two points of
intersection,
one at x = −1 and a second at x = 9.

Figure 7. Using the graphing calculator to solve
the inequality |4 − x| > 5.
The graph of y = |4 − x| lies above the graph of y = 5 for all values of x that
lie
either to the left of −1 or to the right of 9. Hence, the solution of |4−x| > 5
is the set
{x : x < −1 or x > 9}.
Following the guidelines established in Example 7, we create the image
shown in
Figure 8 on our homework paper. Note that we’ve labeled each axis, scaled
each axis
with xmin, xmax, ymin, and ymax, labeled each graph with its equation, and
shaded
and labeled the solution on x-axis.
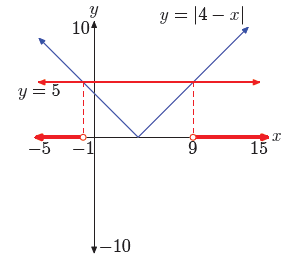
Figure 8. Reporting a graphical solution
of |4 − x| > 5.
Algebraic Approach. Let’s explore an algebraic solution of |4 − x| > 5.
In much
the same manner that |x| > 5 leads to the conditions x < −5 or x > 5, the
inequality
|4 − x| > 5
requires that
4 − x < −5 or 4 − x > 5.
We can solve each of these independently by first subtracting 4 from each side
of
the inequality, then multiplying both sides of each inequality by −1, reversing
each
inequality as we do so.
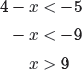 |
or |
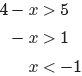 |
We prefer to write this solution in the order
x < −1 or x > 9,
as it then matches the order of the graphical solution shaded in Figure 8.
That is, the
solution set is {x : x < −1 or x > 9}.
The algebraic technique of this last example leads to the following property.
Property 17. If a > 0, then the inequality
|x| > a is equivalent to the compound
inequality x < −a or x > a. |
This property provides a simple algebraic technique for
solving inequalities of the
form |x| > a, when a > 0. Let’s concentrate on this technique in the examples
that
follow.
 Example 18.
Solve the inequality |4x − 3| > 1 for x. Example 18.
Solve the inequality |4x − 3| > 1 for x.
The first step is to use Property 17 to write that
|4x − 3| > 1
is equivalent to
4x − 3 < −1 or 4x − 3 > 1.
We can now solve each inequality independently. We begin by adding 3 to both
sides
of each inequality, then we divide both sides of the resulting inequalities by
4.
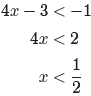 |
or |
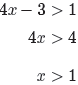 |
We can sketch the solutions on a number line.

And we can describe the solution using interval and
set-builder notation.
(−∞, 1/2) ∪ (1,∞) = {x : x < 1/2 or x > 1}
Again, let a > 0. As we did with |x| ≤ a, we can take the union of the solutions
of
|x| = a and |x| > a to find the solution of |x| ≥ a. This leads to the following
property.
Property 19. If a > 0, then the inequality
|x| ≥ a is equivalent to the inequality
x ≤ −a or x ≥ a. |
 Example 20. Solve the inequality 3|1 − x| − 4 ≥ |1 − x| for x.
Example 20. Solve the inequality 3|1 − x| − 4 ≥ |1 − x| for x.
Again, at first glance, the inequality
3|1 − x| − 4 ≥ |1 − x|
looks unlike any inequality we’ve attempted to this point. However, if we
subtract
|1 − x| from both sides of the inequality, then add 4 to both sides of the
inequality, we
get
3|1 − x| − |1 − x| ≥ 4.
On the left, we have like terms. Note that 3|1−x|−|1−x| = 3|1−x|−1|1−x| =
2|1−x|.
Thus,
2|1 − x| ≥ 4.
Divide both sides of the last inequality by 2.
|1 − x| ≥ 2
We can now use Property 19 to write
1 − x ≤ −2 or 1 − x ≥ 2.
We can solve each of these inequalities independently. First, subtract 1 from
both sides
of each inequality, then multiply both sides of each resulting inequality by −1,
reversing
each inequality as you go.
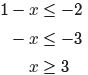 |
or |
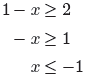 |
We prefer to write this in the order
x ≤ −1 or x ≥ 3.
We can sketch the solutions on a number line.

And we can describe the solutions using interval and
set-builder notation.
(−∞,−1] ∪ [3,∞) = {x : x ≤ −1 or x ≥ 3}
Revisiting Distance
If a and b are any numbers on the real line, then the distance between a and b
is found
by taking the absolute value of their difference. That is, the distance d
between a and
b is calculated with d = |a − b|. More importantly, we’ve learned to pronounce
the
symbolism |a − b| as “the distance between a and b.” This pronunciation is far
more
useful than saying “the absolute value of a minus b.”
 Example 21.
Solve the inequality |x − 3| < 8 for x. Example 21.
Solve the inequality |x − 3| < 8 for x.
This inequality is pronounced “the distance between x and 3 is less than 8.”
Draw
a number line, locate 3 on the line, then note two points that are 8 units away
from 3.
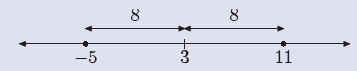
Now, we need to shade the points that are less than 8
units from 3.
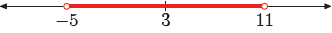
Hence, the solution of the inequality |x − 3| < 8 is
(−5, 11) = {x : −5 < x < 11}.
 Example 22. Solve the inequality |x + 5| > 2 for x.
Example 22. Solve the inequality |x + 5| > 2 for x.
First, write the inequality as a difference.
|x − (−5)| > 2
This last inequality is pronounced “the distance between x and −5 is greater
than 2.”
Draw a number line, locate −5 on the number line, then note two points that are
2
units from −5.

Now, we need to shade the points that are greater than 2
units from −5.
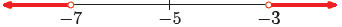
Hence, the solution of the inequality |x + 5| > 2 is
(−∞,−7) ∪ (−3,∞) = {x : x < −7 or x > −3}.
|


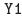 and
and 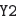 , respectively, as shown in
, respectively, as shown in