Home
Linear Equations and Inequalitie
Solving Inequalities
Absolute Value Inequalities
Graphing Equivalent Fractions Lesson Plan
Investigating Liner Equations Using Graphing Calculator
Graphically solving a System of two Linear Equatio
Shifting Reflecting Sketching Graph
Graphs of Rational Functions
Systems of Equations and Inequalities
Graphing Systems of Linear Equat
LINEAR FUNCTIONS: SLOPE, GRAPHS AND MODELS
Solving Inequalities with Absolute Values
Solving Inequalities
Solving Equations & Inequalities
Graph the rational function
Inequalities and Applications
Inequalities
Using MATLAB to Solve Linear Inequalities
Equations and Inequalities
Graph Linear Inequalities in Two Variables
Solving Equations & Inequalities
Teaching Inequalities:A Hypothetical Classroom Case
Graphing Linear Inequalities and Systems of Inequalities
Inequalities and Applications
Solving Inequalities
Quadratic Inequalities
Inequalities
Solving Systems of Linear Equations by Graphing
Systems of Equations and Inequalities
Graphing Linear Inequalities
Inequalities
Solving Inequalities
Solving Inequalities
Solving Equations Algebraically and Graphically
Graphing Linear Equations
Solving Linear Equations and Inequalities Practice Problems
Graphing Linear Inequalities
Equations and Inequalities
Solving Inequalities

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Inequalities

Section 3.2 Linear Programing Problems.

Be sure that you define your variables as shown in class. I am very picky about this and will deduct points
if you don't do it correctly.

Word Problems for Section 3.2

Set up the following linear programing problems. Do not solve.

1. A 4-H member raises only geese and pigs. She wants to raise no more than 16 animals, including no
more than 10 geese. She spends $5 to raise a goose and $15 to raise a pig, and she has $180 available
for this project. The 4-H member wishes to maximize her profits. Each goose produces $6 in pro t
and each pig $20 in pro t. How many of each animal should be raised?

2. The Hi-Fi Record Store is about to place an order for cassette tapes and compact disks. The distributor
from which they order requires that each order must request at least 250 items. The prices that Hi-
must pay are $3.50 for each cassette and $7.50 for each compact disk. The distributor also requires
that at least 30% of any order be for compact disks. How many cassettes and how many compact
disks should Hi-Fi order so that its total ordering costs will be kept to a minimum?

3. The Acrosonic Company manufactures a model G loudspeaker system in plants I and II. The output
at plant I is at most 800 systems per month, whereas the output at plant II is at most 600 per
month. These loudspeaker systems are shipped to the three warehouses{A, B, and C{whose minimum
monthly requirements are 500, 400, and 400, respectively. Shipping costs from plant I to warehouse
A, warehouse B, and warehouse C are $16, $20, and $22 per loudspeaker system, respectively, and
shipping costs from plant II to each of these warehouses are $18, $16, and $14, respectively. What
shipping schedule will enable Acrosonic to meet the warehouses' requirements and at the same time
keep its shipping costs to a minimum?

Section 3.1 Inequalities

• Note: if you multiply or divide an inequality by a negative number, then you must flip the sign.

• The feasible region is the set of points that satisfy the system of inequalities, i.e. makes the inequal-
ities true. Sometimes this is called the solution set.

• When graphing inequalities use a solid line for ≥ or ≤ and use a dashed line for < or >.

• There are two methods for nding feasible regions. One method is to shade the feasible region. This
technique is shown in the book. The other method is the scratch-o method(shading the un-feasible
regions). When working with more than one inequalities, the scratch-o method makes the problem
a little bit easier to work.

• To nd the feasible region (of a single inequality):

1. Graph the line represented by the inequality: solid line for ≥ or ≤ and dashed line for < or >.

2. Pick a point from one side of the inequality and plug the point into the inequality. Be sure that
is not on the line.

3. If the point makes the inequality true, then scratch o the side that did not contain the point
you picked. If the point makes the inequality false then scratch o the side that contained the
point you picked.

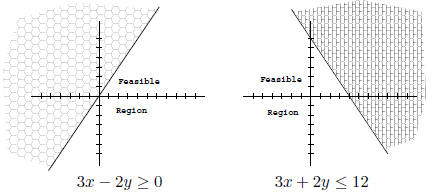
4. The side of the inequality that is not scratched o is the feasible region. Label it with: Feasible
Region or FR.

Example 1: Here are feasible regions for the inequalities 3x − 2y ≥ 0 and 3x + 2y ≤ 12.

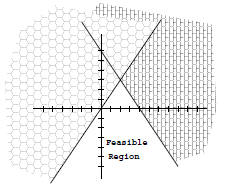
If your system of inequalities has more than one inequality, then the feasible region is the part of the
graph that doesn't get scratched o .

Example 2: Here is the feasible region for the system of inequalities: 3x − 2y ≥ 0 and 3x + 2y ≤ 12.

• Shading with the Calculator. First solve the inequality for y. Remember if you multiply or divide
by a negative number then flip the sign. Then press and type the formula into Y₁. Once this is
done move the cursor to symbol just before Y₁. As you press , the calculator will toggle thru
its di erent styles of graphing. If your inequality was y ≥ then select to scratch o what is greater.
If your inequality was y ≤ then select to scratch o what was less. Once you have selected your
graphing style, then you can graph the feasible region.

• A feasible region is bounded (fenced in) if it can be enclosed by a circle. Otherwise it is unbounded.

Section 3.3 Method of Corners.

• A corner point is a point on the edge of the feasible region where two inequalities in the system of
inequalities intersect.

• Theorem: Given a feasible region, called R, and an objective function f = ax + by

- If the objective function has a maximum or a minimum then it will happen at a corner point.
- If R is bounded, then f will have both a maximum and a minimum.
- If R is unbounded, then f may or may not have a maximum or a minimum.
- If R is unbounded, a > 0, b > 0, and x; y ≥ 0, then f will have a minimum.

• If the feasible region is bounded, just plug all of the corner points into the objective function and see
which point or points will give the desired result.

• If there are two points, A and B, where the objective function has a maximum(minimum), then all
points on the line segment connecting A and B are also a maximum(minimum).

• If a feasible region is unbounded, then you will have to analyze whether or not the objective function
has a maximum or a minimum.