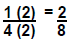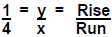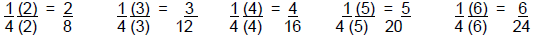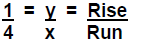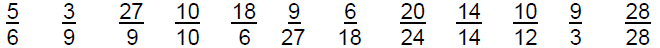|
|
Graphing Equivalent Fractions Lesson Plan
Aim:
Students will learn to graph families of equivalent fractions and to compare
them by observing the slope of the line formed by each fraction family.
Specific Objectives:
Students will learn to:
o Find equivalent fractions for a given fraction (brief review)
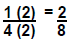
o Plot a fraction on a grid, e.g.,
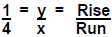
o Plot some equivalents for the initial fraction
o Connect the points for a family of equivalent fractions by drawing a straight
line that goes through the origin
o Observe the slope of the line drawn
o Place fractions in ascending order by comparing the slopes of each line (the
greater the fraction, the steeper the slope) after several families of
equivalent fractions have been graphed
o Observe that fractions and their reciprocals will form lines equidistant from
the line for 1 and that the angles formed will be the same.
Materials/Supplies:
Teacher:
o Drawings or transparencies to review equivalent fractions, e.g., 1/4, 2/8,
4/16, 5/20, 6/24
o Overhead projector
o Overhead markers
o Transparency of a grid
o Transparency of answers for independent practice activity (grid and fractions
in ascending order
o Ruler
o Vocabulary list (fraction, equivalent fractions, slope, origin, ascending
order, descending order, reciprocal fractions)
Students:
o 2 grids per student
o 1 ruler per student
o Pencils and colored pencils
Lesson:
o Time: approximately 40-45 minutes
o Introduction: Review equivalent fractions
o Tell story of Cedric’s birthday parties. Class discussion will generate
answers. When Cedric was 4, he invited 3 friends to his party, and they all came
(total of 4 children present), so each child got ? of cake? (¼) . When he was 8,
Cedric invited 7 friends, but only 3 came again because the rest were on
vacation. He cut the cake into 8 pieces, but since there were only 4 at the
party, each child got ? of the cake? (2/8 or ¼) . When he turned 12, he invited
11 friends, but again only 3 came! (Poor Cedric!) This time each child got ? of
the cake? (3/12 or ¼). He tried again when he was 16—same story, so each person
got ? of the cake? (4/16 or ¼) and he tried again when he was 20, so each person
got ? of the cake? (5/20 or ¼). When he was 24, he decided to invite just 3
friends and they all came! (Each person got ? of the cake—¼, but if he had cut
the cake into 24 pieces, each person would have gotten ? of the cake? (6/24).
o Review formation of equivalent fractions and concept of
a fraction family
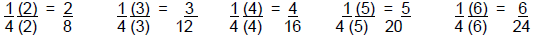
o We can call a group of equivalent fractions a fraction
family.
Activities:
o Class learns to plot a fraction on a grid through teacher
demonstration/explanation:
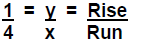
Teacher (using overhead) and class work together to plot
the fraction equivalents for ¼ that were introduced in the story (2/8, 3/12,
4/16, 5/20, 6/24) and to connect the points with a line through the origin.
o Guided practice
Students generate some equivalents for ½ (e.g., 2/4, 3/6, 4/8, 6/12) and then
they graph them (along with teacher at overhead projector). They do the same for
¾ (e.g., 6/8, 9/12, 12/16, 15/20) , and 1 (1/1, 2/2, 3/3, 4/4, 5,5). Teacher
introduces concept of reciprocal fractions, and they graph reciprocals for
fraction family of ¼ (4/1, 8/2, 12/3, 16/4, 20/5). Use page 4.
Class discussion to answer the question, “If we did not
know the value of these fractions, how could we use the graph we made to put the
fractions in ascending (growing larger) or descending (growing smaller) order?
(Fractions get larger as line gets closer to the y axis.) Fractions are then
listed in ascending order. Review slope and then continue the discussion to
answer the question, “When we compare the slopes of the lines formed by several
different sets or families of fractions, what is the relationship between the
slope and the size of the fractions? (The steeper the slope, the larger the
fraction.) Finally, students will look at the angle formed by the line for the
family of fractions representing ¼ and 1/1 and compare it to the angle formed by
the family of fractions representing 4/1. (Angles are the same.) See page 5.
o Independent practice (This could be done the next day.)
Students are given a list of fractions to plot on a grid (5/6, 3/9, 27/9, 10/10,
18/6, 9/27, 6/18, 20/24, 14/14, 10/12, 9/3, 28, 28). Students must connect
points to draw lines through the origin. Hint: They will need to draw 4
different lines. Finally, they will list the fractions in ascending order.
(Note: It is important the grid be large enough and the fractions be far enough
apart in size to allow the students to easily connect the points to draw lines
through the origin. In addition, at this stage it is helpful to use fractions
that are simple enough so that students could determine which ones are
equivalent even without the graph.) Use pages 4 and 6
o Follow-up
Students correct their answers with the graph that is on an overhead
transparency. Review of questions asked previously during guided practice.
o Extension
Give students a graph with lines already drawn and ask them to list equivalent
fractions (in ascending or descending order) based on the graph. Use page 5 and
7.
Activity: Graphing Equivalent Fractions
1. Plot the following fractions on a grid:
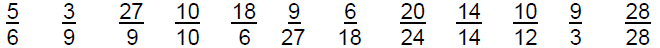
2. Draw lines to connect points with the origin. (Hint: 4
lines in all.)
3. List families of equivalent fractions in ascending order.
Answers:
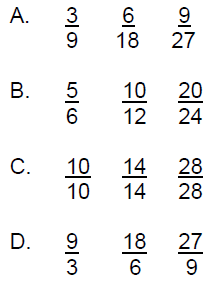
|